INECUACIONES

 INECUACIONES 

Las inecuaciones de primer grado son aquellas cuya incógnita, en este caso única, tiene exponente 1. Si a los dos miembros de una inecuación les sumo o les resto un número o una misma expresión algebraica, obtendremos una inecuación equivalente.

• Una inecuación es una desigualdad algebraica en la que aparecen una o más incógnitas en los miembros de la desigualdad.
• La solución de una inecuación lineal se puede representar haciendo uso de intervalos en la recta numérica, que contiene infinito en números reales. 

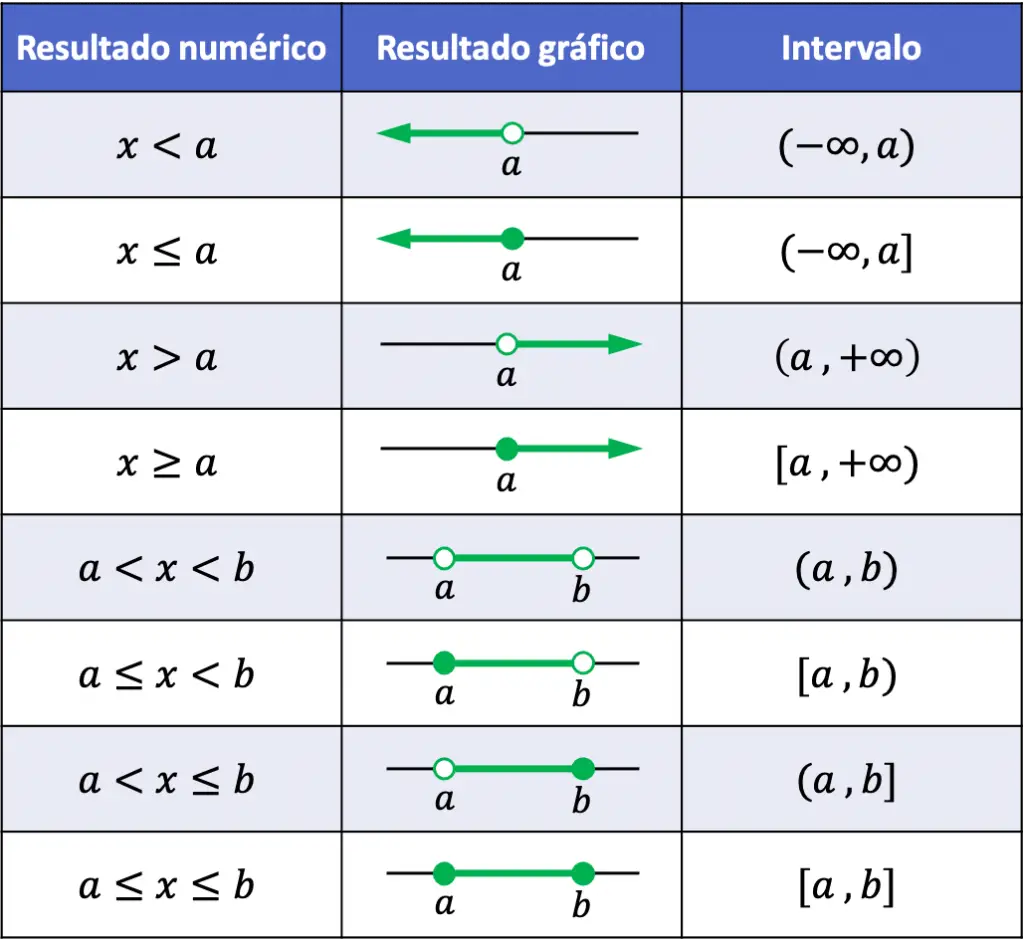
INTERVALO ABIERTO

• ( )
• Menor y mayor qué < >
• En la gráfica O

INTERVALO CERRADO 

• [ ]
• Menor igual y mayor o igual ≤ ≥
• 📀

GRÁFICA 

REGLA PRINCIPAL 

Si multiplicamos la inecuación por un número negativo, obtenemos una equivalente si cambiamos el sentido. Es decir, si queremos multiplicar por (-) para que nuestra incógnita sea positiva, cambiamos el ángulo de la desigualdad (signo mayor o menor). 

Regla 1: Al sumar o restar una misma cantidad a los dos miembros de una inecuación, se obtiene una inecuación equivalente. Regla 2: Al multiplicar o dividir por una misma cantidad positiva los dos miembros de una inecuación, se obtiene otra equivalente.

Grafica 

$x \leq 4$x, is less than or equal to, 4

$\llap{-}5$$\llap{-}4$$\llap{-}3$$\llap{-}2$$\llap{-}1$$0$$1$$2$$3$$4$$5$

Grafica

x <0

$\llap{-}5$$\llap{-}4$$\llap{-}3$$\llap{-}2$$\llap{-}1$$0$$1$$2$$3$$4$$5$

Grafica 

$x \geq -1$x, is greater than or equal to, minus, 1

$\llap{-}5$$\llap{-}4$$\llap{-}3$$\llap{-}2$$\llap{-}1$$0$$1$$2$$3$$4$$5$

Grafica 

$x <1$x, is less than, 1

$\llap{-}5$$\llap{-}4$$\llap{-}3$$\llap{-}2$$\llap{-}1$$0$$1$$2$$3$$4$$5$

Se dice que son de primer grado cuando dicha letra no está elevada a ninguna potencia (por tanto a 1).

Ejemplo:

• 1 - 3x = 2x - 9.
• x - 3 = 2 + x.
• x/2 = 1 - x + 3x/2.

Un sistema de inecuaciones con dos incógnitas tiene como solución uno de los semiplanos que resulta de representar la ecuación resultante, que se obtiene al transformar la desigualdad en una igualdad.

Pasos para resolver inecuaciones con dos incógnitas

Vamos a resolver la inecuación:

1 Transformamos la desigualdad en igualdad.

2 Damos a una de las dos variables dos valores, con lo que obtenemos dos puntos.

3 Al representar y unir estos puntos obtenemos una recta.

4 Tomamos un punto, por ejemplo el , los sustituimos en la desigualdad. Si se cumple, la solución es el semiplano donde se encuentra el punto, si no la solución será el otro semiplano.

Casos posibles de inecuaciones

Menor o igual

Tomamos el punto y lo sustituimos en la inecuación.

Como se cumple la desigualdad la solución es el semiplano donde se encuentra , incluyendo la recta porque tomamos los puntos menores y también los iguales. En este caso dibujamos la recta con trazo continuo

Menor

Tomamos el punto y lo sustituimos en la inecuación.

Como se cumple la desigualdad la solución es el semiplano donde se encuentra

En este caso (menor que, pero no igual) los puntos de la recta no pertenecen a la solución

En este caso dibujamos la recta con trazo discontinuo

Mayor

Tomamos el punto y lo sustituimos en la inecuación.

No

Como no se cumple la desigualdad, la solución es el semiplano donde no se encuentra

En este caso (mayor que, pero no igual) los puntos de la recta no pertenecen a la solución.

En este caso dibujamos la recta con trazo discontinuo

Mayor o igual

Tomamos el punto y lo sustituimos en la inecuación.

No

Como no se cumple la desigualdad, la solución es el semiplano donde no se encuentra

En este caso (mayor o igual) los puntos de la recta pertenecen a la solución.

En este caso dibujamos la recta con trazo continuo

                   INECUACIONES DOBLES 

Método 1:

Todos los signos de las inecuaciones deben ser <, ≤  no puede incluir >, ≥.

Método 2:

Debe incluir dentro de los valores de la inecuación de un signo >, ≥.

EJEMPLOS 

• 3<X+1<7

3-1<X<7-1

2<X<6

Intervalo  (-∞,2)(-∞,6)

• 5≤ 3x -7<14

5+7≤ 3x <14+7

12≤ 3x <21

12/3≤ x <21/3

4≤ x <7

[4,-∞)(-∞,7)

• 2≤x+2>7

2≤x+2>7

x+2>7

x>7-2

x>5

2≤x+2

2-2≤x

0≤x

• -3>3x-2≥-11

-3>3x-2

-3+2>3x

-1/3>x

3x-2≥-11

3x≥-11+2

x≥-9/3