Geometría

Punto, línea y plano son los elementos geométricos básicos con los que podemos dibujar todas las figuras geométricas.

Se denominan propios si pertenecen a un espacio finito e impropios si están en el infinito.

Los límites de un cuerpo son las superficies, de las superficies las líneas y de las líneas los puntos.

Los planos tienen dos dimensiones, una sola dimensión las líneas y ninguna dimensión los puntos, que únicamente determinan un lugar.
Punto

Queda definido por la intersección de dos líneas, se designa con letra mayúscula.
Recta

Línea recta: es una sucesión de puntos alineados sin principio ni final. Se designa con letra minúscula.

Hay dos subtipos:
Se denomina semirrecta a la recta cuando esta tiene un origen concreto en un espacio finito (propio) y el otro extremo está en el infinito (impropio).
Se denomina segmento cuando está limitada por ambos extremos por puntos.
Plano

Está formado por infinitas rectas y no tiene límites.

Se designa con letra mayúscula –a menudo del alfabeto griego–.

Es la superficie llana, lisa que se extiende indefinidamente en todas las direcciones de la superficie.

Queda determinado por:

• 2 rectas que se cortan
• Un punto y una recta no alineados
• Tres puntos no alineados
• Dos rectas paralelas.

ÁNGULOS SEGÚN SUS MEDIDAS 

1) Ángulo agudo: es aquel que mide más de 0° y menos de 90°.





2) Ángulo recto: es aquel que mide 90°.





3) Ángulo obtuso: es aquel que mide más de 90° y menos de 180°.





4) Ángulo llano: es aquel que mide 180°.





5) Ángulo completo: es aquel que mide 360°.

6) Ángulos cóncavos: tienen una amplitud de más de 180º y menos de 360º. Para medirlos usarás un transportador circular.

7) Ángulo nulo: es aquel que mide 0º

 ÁNGULOS SEGÚN SUS           MEDIDAS 

Ángulos complementarios son los ángulos que su suma es igual a 90 grados. Complemento de un ángulo es lo que le falta al ángulo es lo que le falta al ángulo para medir un ángulo recto. Decimos que dos ángulos son complementarios si su suma forma un ángulo recto, es decir, 90º.

 

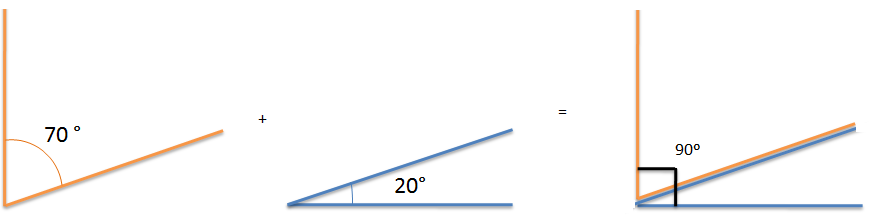
En este caso 70 ° y 20 ° son complementarios porque 70° + 20° = 90°.

Más ejemplos podrían ser 47° y 43°, ya que 47° + 43° = 90°, 30° y 60°,  45° y 45° , etc.

Ángulos suplementarios son los ángulos que se suma es igual a 180 grados. Suplemento de un ángulo es lo que le falta al angulo para medir un ángulo plano o llano. Dos ángulos son suplementarios si su suma forma un ángulo llano, es decir, 180°.

160° y 20° son suplementarios porque suman 180°.

110° y 70° también lo son ya que 110° + 70° = 180°, lo mismo para 25° y 155°.

Α α Alfa	Β β Beta	Γ γ Gamma
Δ δ  Delta     Θ θ Theta

formula:

A+B+C=180 

A+B+C=90

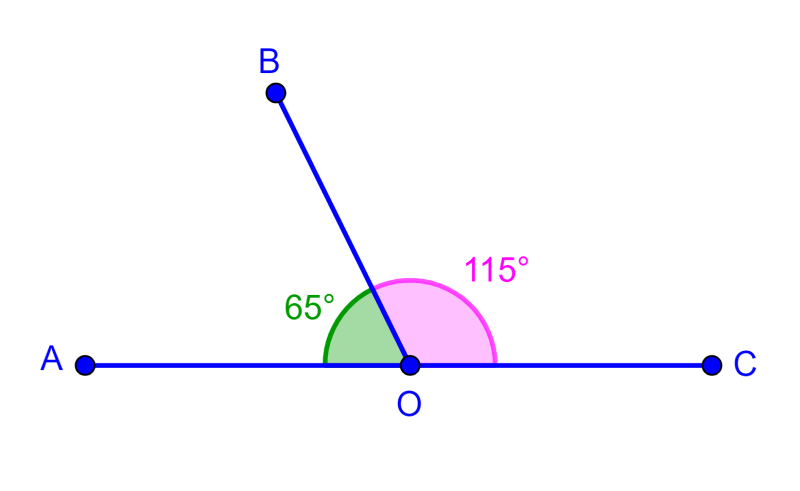
              ÁNGULOS SUPLEMENTARIOS 

A+115=180 

A=180 -115

A=65

A+108,9=180 

A=180 -108,9

A=71,1 

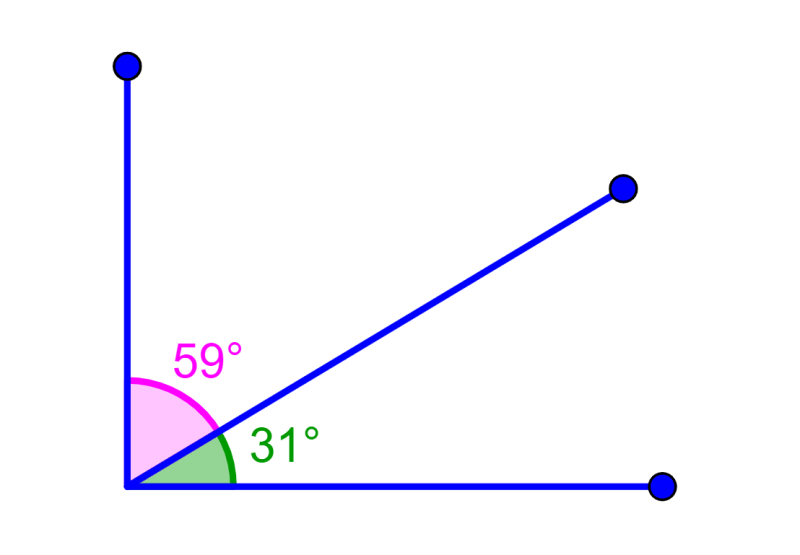
            ÁNGULOS COMPLEMENTARIOS

A+57=90

A=90-57

A=33

 A+59=90

A=90-59

A=31

 A+60=90

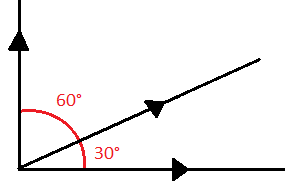
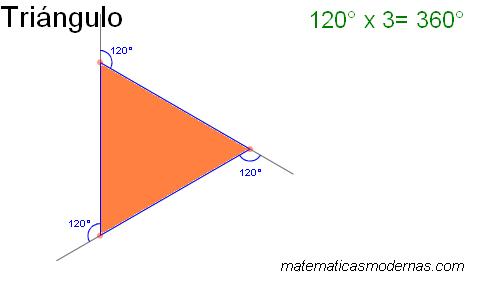
A=90-60

A=30 

   ÁNGULOS INTERNOS DE UN TRIANGULO

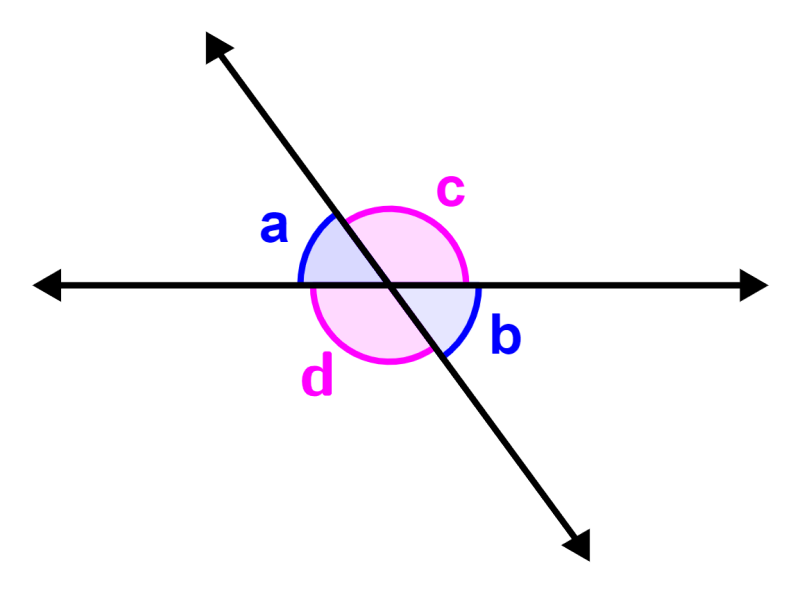
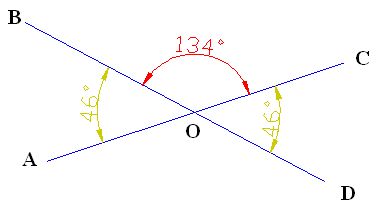
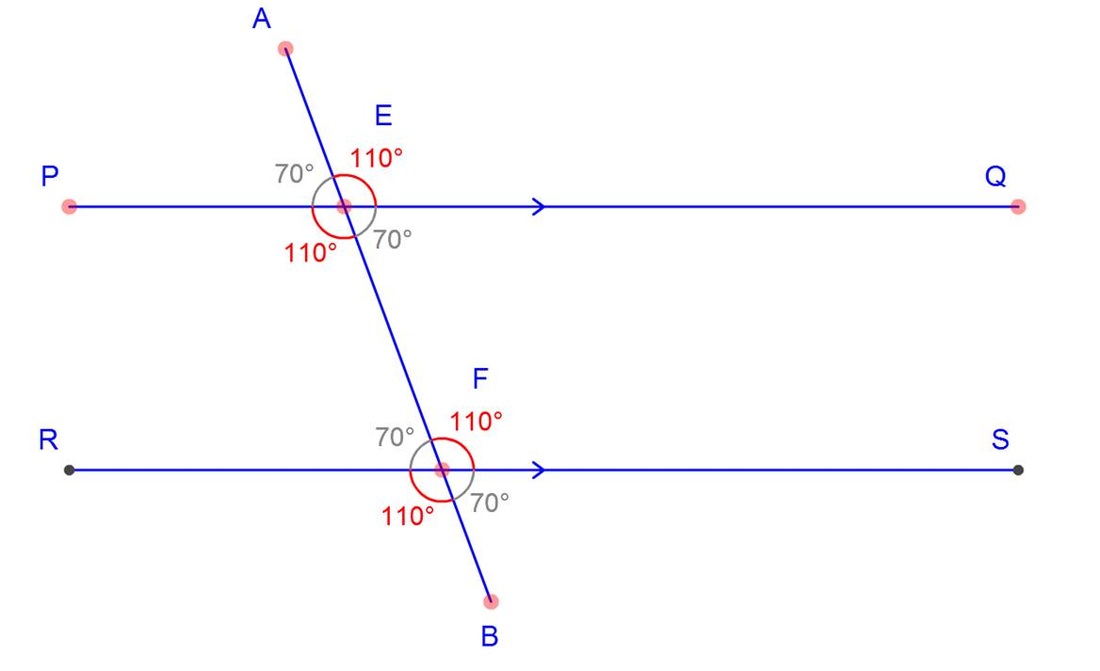
Cada vértice del polígono se corresponde con un ángulo interior y uno exterior, siendo ambos suplementarios, es decir, suman 180º.

 

 

  ÁNGULOS EXTERNOS DE UN TRIANGULO

Los ángulos exteriores de un triángulo lo forman un lado y su prolongación. El valor de un ángulo exterior de un triángulo es igual a la suma de los dos interiores no adyacentes. Un ángulo interior y exterior de un triángulo son suplementarios, es decir, suman 180º.

 ÁNGULOS OPUESTOS AL VERTICE Y   ÁNGULOS EN DOS RECTAS

Dos ángulos opuestos por el vértice son los ángulos opuestos cuando se cruzan dos rectas.

En la figura, y son ángulos opuestos por el vértice. Lo interesante es que los ángulos opuestos son iguales: (de hecho son congruentes).

   ÁNGULOS CON RECTAS PARALELAS Y UNA TRANSVERSAL

Si una recta transversal corta a dos rectas paralelas: Ángulos alternos internos: son los ángulos que están entre las paralelas y a distinto lado de la transversal. Ángulos alternos externos: son los ángulos que están en la parte exterior de las paralelas y a distinto lado de la transversal.